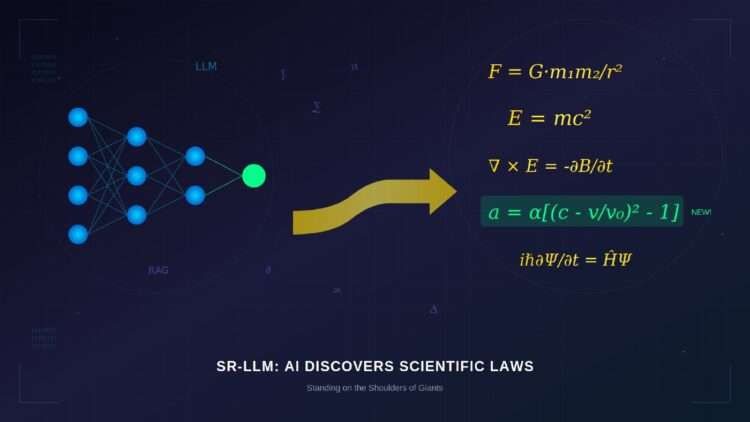
A new framework combines large language models with deep learning to discover scientific equations, outperforming all existing methods on physics benchmarks.
For millennia, scientists have searched for elegant equations that capture nature’s laws. Now, an AI system can do it too—not by brute force, but by learning from humanity’s accumulated knowledge and building upon it, much like a scientist standing on the shoulders of giants.
The Ancient Dream of Automated Discovery
In 1687, Isaac Newton published the Principia Mathematica, revealing that a single equation could explain both the fall of an apple and the orbit of the Moon. That equation—the law of universal gravitation—took humanity’s greatest mind years to derive. But what if a machine could discover such laws automatically, simply by observing data?
This dream has tantalized researchers for decades. In the 1990s, critics argued that artificial neural networks, for all their pattern-recognition prowess, could never discover fundamental physical laws. The networks could fit data beautifully, but the result was an impenetrable tangle of weights and biases—nothing resembling the clean, interpretable equations that scientists prize.
Then came symbolic regression: the attempt to have computers search for mathematical formulas that best describe observed data. Unlike traditional regression, which fits parameters to a predetermined equation form, symbolic regression discovers the equation itself. The approach has achieved some notable successes, rediscovering laws like Kepler’s third law of planetary motion from raw orbital data. But a fundamental problem remained: the search space of possible equations is essentially infinite. How do you find a needle in a haystack that extends forever in every direction?
Now, an international team of researchers from Tsinghua University, the Chinese Academy of Sciences, the University of Southern California, and other institutions has developed a system that tackles this challenge in a remarkably human way. Their framework, called SR-LLM, doesn’t just search blindly through mathematical possibilities. It learns from humanity’s accumulated scientific knowledge, builds upon past discoveries, and uses that foundation to find new equations more efficiently than any previous method.
Learning Like a Scientist
The key insight behind SR-LLM is deceptively simple: scientists don’t discover laws in a vacuum. When Einstein developed general relativity, he built upon Newton’s mechanics, Riemann’s geometry, and Maxwell’s electromagnetism. When Darwin formulated natural selection, he drew on Malthus’s population dynamics and Lyell’s geology. Great discoveries emerge from the synthesis of existing knowledge applied to new observations.
According to research published in PNAS, SR-LLM captures this process computationally through a technique called retrieval-augmented generation, or RAG. Originally developed to improve large language models like ChatGPT, RAG allows an AI system to query an external knowledge base and incorporate relevant information into its reasoning. For SR-LLM, this knowledge base contains the accumulated wisdom of scientific equation-building: what kinds of terms tend to appear together, what mathematical structures have proven useful in the past, and why certain combinations make physical sense.
The system works through four interconnected stages. In the Sampling stage, a deep reinforcement learning algorithm proposes candidate equations by selecting symbols—variables, constants, and operations—and assembling them into mathematical expressions represented as tree structures. In the Calibration stage, the system fits the free parameters in each candidate equation to the observed data using a two-stage optimization process designed to balance speed with precision. In the Evaluation stage, candidates are scored based on how well they fit the data, how similar they are to known expert models, and how complex they are. Finally, in the Updating stage, the large language model analyzes successful equations, extracts insights about why certain symbol combinations work well, and stores this knowledge for future use.
This last stage is where SR-LLM truly distinguishes itself. The LLM doesn’t just generate new symbol combinations randomly—it reasons about them. Given a high-performing mathematical term discovered during the search, the system retrieves similar concepts from its knowledge base, generates hypotheses about how to extend or modify that term, and explains its reasoning in natural language. When a promising new equation is found, the system reflects on why it works, extracting generalizable principles that can guide future searches.
The AlphaGo of Equation Discovery
The researchers explicitly compare their approach to DeepMind’s AlphaGo, the system that defeated world Go champion Lee Sedol in 2016. Just as AlphaGo learned from millions of human game records before developing superhuman strategies, SR-LLM absorbs the equation-building knowledge embedded in centuries of scientific literature. And just as AlphaGo combined this learned intuition with Monte Carlo tree search to explore promising moves, SR-LLM combines LLM-derived knowledge with deep reinforcement learning to explore promising equation structures.
The comparison is more than rhetorical. Both systems face combinatorial search spaces so vast that brute-force exploration is hopeless. Both use neural networks to learn which choices are worth exploring. And both achieve performance that surpasses what either pure learning or pure search could accomplish alone.
To validate their approach, the researchers tested SR-LLM on two standard benchmarks. The first, called “Fundamental-Benchmark,” consists of 100 mathematical expressions of varying complexity without physical dimensions—a pure test of search capability. Without any LLM assistance, SR-LLM matched or exceeded all previous symbolic regression methods except one brute-force approach that explores vastly more candidates in the same time.
The second benchmark is where SR-LLM truly shines. The “Feynman-Benchmark” contains 100 classical physics formulas with clear physical meanings—equations like Newton’s second law, the ideal gas law, and the relativistic energy-momentum relation. Here, the system was allowed to use its full LLM-powered knowledge integration.
The results were striking. SR-LLM achieved a 76.1% exact recovery rate, meaning it rediscovered the precise symbolic form of over three-quarters of the physics equations from data alone. This significantly outperformed all other methods tested, including previous state-of-the-art approaches. The combination of physical knowledge guidance and intelligent search proved far more powerful than either component alone.
Discovering What Scientists Couldn’t
But SR-LLM isn’t just about rediscovering known equations. The researchers also tested whether it could find genuinely new models in a domain where the optimal formulation remains controversial: how do human drivers follow the car in front of them?
Car-following behavior might seem mundane compared to discovering laws of physics, but it’s a surprisingly deep problem. For over 70 years, traffic scientists have proposed mathematical models describing how drivers adjust their speed based on the distance to the preceding vehicle, relative velocity, and other factors. Classic models like the Intelligent Driver Model (IDM), the GHR model, and the Helly model are widely used in traffic simulation. Yet none perfectly captures the complexity of real human driving behavior, and the “true” equation—if one exists—remains unknown.
The researchers fed SR-LLM trajectory data from 108 car-following vehicle pairs recorded in the Next Generation Simulation (NGSIM) program, a dataset notorious for its measurement noise and the variability of human driving styles. They provided the system with knowledge of three classic car-following models and asked it to discover new equations that might fit the data better while remaining interpretable.
SR-LLM succeeded on both fronts. It rediscovered the classic Helly and IDM models from the noisy empirical data—something the comparison method, PhySO, failed to do even after exploring one million candidate equations. More importantly, it discovered entirely new car-following models that had never appeared in the 70-year literature on the subject. These new models achieved higher fitting accuracy than the classic models while maintaining clear physical interpretability. One discovered model overcame a known limitation of the IDM—its tendency to overdecelerate during sudden speed changes—producing more realistic simulated trajectories.
Why It Works: Standing on Giants’ Shoulders
The power of SR-LLM comes from how it reduces the effectively infinite search space of possible equations to something manageable. The researchers provide an elegant mathematical argument: if your expression library contains η symbols and the shortest equation that fits your data requires l symbols, then a brute-force search must explore up to η^l candidates. Adding new, more complex symbols to the library—composite terms that combine multiple basic symbols—increases η slightly but can dramatically reduce l. If adding η’ new symbols reduces the minimum expression length by l’, the search space shrinks by a factor of approximately 1/η^l’, which can be enormous.
This is exactly what SR-LLM’s knowledge-driven approach accomplishes. By having the LLM identify and generate useful composite symbols—terms that frequently appear in successful equations—the system effectively compresses the search space. Instead of searching for individual symbols that might combine to form a useful expression, it searches over higher-level building blocks that already encode successful patterns.
The framework also addresses a persistent challenge in symbolic regression: balancing accuracy against interpretability. Many machine learning approaches can fit data arbitrarily well by generating increasingly complex expressions, but the results become meaningless to human scientists. SR-LLM explicitly penalizes complexity and rewards similarity to known expert models, guiding the search toward equations that humans can understand and verify.
Perhaps most remarkably, the system can explain its discoveries. When SR-LLM finds a high-performing equation, the LLM component can decompose it hierarchically, explaining why each term contributes to the model’s success and how the overall structure relates to known physical principles. This transforms symbolic regression from a black-box search into a collaborative discovery process where humans and machines can learn from each other.
The Future of Machine-Assisted Discovery
The researchers envision SR-LLM as a stepping stone toward fully autonomous scientific discovery. While the current system relies on human-provided prior knowledge to guide its search, its architecture could in principle support “cold-start” operation—building its own knowledge base from scratch through iterative self-refinement, similar to how AlphaZero learned to play Go without any human game records.
Such a system could potentially discover equations that no human has ever conceived, not by lucky accident but through systematic exploration of mathematical structures that humans would never think to try. It could identify subtle patterns in data that escape human intuition, suggest new theoretical frameworks, and even propose experiments to test its hypotheses.
For now, SR-LLM represents a powerful tool for accelerating human scientific discovery. By encoding centuries of mathematical knowledge in a form that machines can access and apply, it allows researchers to build upon the accumulated wisdom of history’s greatest scientists. Isaac Newton famously said that if he had seen further, it was by standing on the shoulders of giants. SR-LLM suggests that machines might soon stand on those same shoulders—and perhaps see further still.
Sources:
- Guo, Z., et al. (2025). “SR-LLM: An incremental symbolic regression framework driven by LLM-based retrieval-augmented generation.” PNAS, 122(52), e2516995122. https://doi.org/10.1073/pnas.2516995122
- Silver, D., et al. (2016). “Mastering the game of Go with deep neural networks and tree search.” Nature, 529, 484–489. https://doi.org/10.1038/nature16961
- Treiber, M., Hennecke, A., & Helbing, D. (2000). “Congested traffic states in empirical observations and microscopic simulations.” Physical Review E, 62, 1805. https://doi.org/10.1103/PhysRevE.62.1805
- Lewis, P., et al. (2020). “Retrieval-augmented generation for knowledge-intensive NLP tasks.” Advances in Neural Information Processing Systems, 33, 9459–9474. https://proceedings.neurips.cc/paper/2020/hash/6b493230205f780e1bc26945df7481e5-Abstract.html